Parábolas

 Definición geométrica de una parábola

Una parábola es el conjunto de puntos del plano que son equidistantes con un punto fijo F (llamado foco) y una recta fija l (llamada directriz).

En la siguiente figura se ilustra esta definición. El vértice V de la parábola se encuentra a la mitad entre el foco y la directriz, y el eje de simetría es la recta que corre por el foco perpendicular a la directriz.

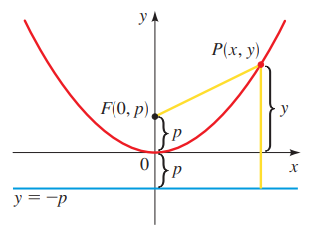
En esta parte restringiremos nuestra atención a parábolas que están situadas con el vértice en el origen y que tienen un eje de simetría vertical u horizontal. Más adelante se estudiarán parábolas en posiciones más generales. Si el foco de dicha parábola es el punto F(0, p), entonces el eje de simetría debe ser vertical y la directriz tiene la ecuación y = -p. La siguiente figura ilustra el caso p > 0.

Deducción de la ecuación de una parábola. Si P(x, y) es cualquier punto en la parábola, entonces la distancia de P al foco  F(usando la fórmula de la distancia) es 

La distancia de P a la directriz es

Por la definición de una parábola estas dos distancias deben ser iguales:

Si p > 0, entonces la parábola abre hacia arriba; pero si p < 0, abre hacia abajo. Cuando x se sustituye por -x la ecuación permanece sin cambio, de modo que la gráfica es simétrica respecto al eje y.

Ecuaciones y gráficas de parábolas

El recuadro siguiente resume lo que acabamos de demostrar acerca de la ecuación y las características de una parábola con eje vertical.

Reflejar la gráfica de la segunda imagen respecto de la recta diagonal y = x tiene el efecto de intercambiar las funciones de x y y. Esto resulta en una parábola con eje horizontal.

Por el mismo método anterior podemos demostrar las siguientes propiedades.

Aplicaciones

Las parábolas tienen una importante propiedad que las hace útiles como reflectores para lámparas y telescopios. La luz de una fuente colocada en el foco de una superficie con sección transversal parabólica se reflejará de modo tal que viaja paralela al eje de la parábola. Entonces, un espejo parabólico refleja la luz en un haz de rayos paralelos. Recíprocamente, la luz que se aproxima al reflector en rayos paralelos a este eje de simetría se concentra en el foco. Esta propiedad de reflexión, se puede demostrar mediante el cálculo, se utiliza en la construcción de telescopios reflectores.